前言

在學習時間序列模型時，我們了解到無論是長短期記憶還是循環神經網路，在經過多個時序運算後，都有可能出現梯度消失的問題。這意味著當我們的輸入到達最後一個隱藏狀態時，原始資料可能已經經歷了一定程度的失真。因此，在Seq2Seq模型中Enocder所給予的上下文向量便是這一個狀態。

而在Decoder中，則需要使用這個上下文向量作為其初始的隱藏狀態來生成文字。這樣做會導致生成越靠近前側的時序被模型遺忘，使得接近結尾的部分可能產生錯誤。因此我們需要找到一種改善的方法，這種方法就是Attention（注意力機制）。

Seq2Seq + Attention

Attention的核心思想是，Decoder在每一步生成輸出時，不是只依賴一個固定的上下文向量，而是根據當前Decoder的時序，動態地計算出Encoder所拋出的上下文向量哪一個是更重要的。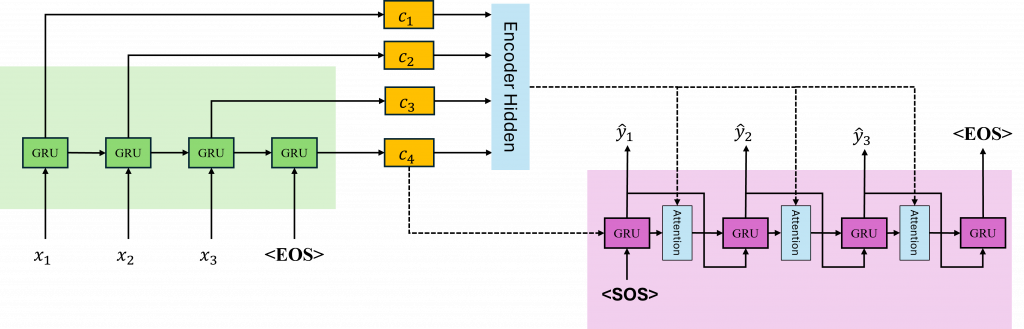

其計算概念是先對Encoder當前的上下文向量c(t)和Decoder上一個時間點的上下文向量c(t-1)進行運算。這種運算方式有很多種，例如：我們可以直接將兩個向量相加、結合或相乘。只要有一種方式能夠將其資訊融合即可。其中最廣為人知的算法就是Bahdanau Attention算法。該算法實際上是我們在循環神經網路中用來計算概率分佈的方法，其數學公式如下：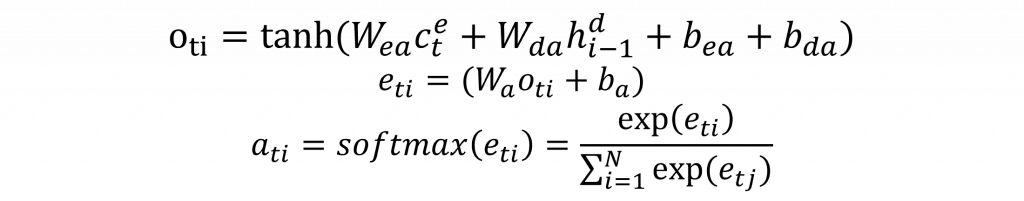

而這次看到這個公式後，你應該能夠完全理解其數學表達和程式的執行方式了。簡單來說，就是先將Encoder與Decoder各自的資訊融合，再將這個機率分佈狀態通過全連接層轉換成對應的資料，最後由softmax函數轉換成各自的機率。這樣我們就可以獲取一個包含所有時序狀態的注意力權重(Attention Weights)矩陣了。

這時注意力權重會產生一個與上下文向量長度相等的矩陣。然後我們只需將每一個上下文向量與注意力權重相乘。這樣，當注意力權重越大時，對應的Encoder上下文向量會保留更多信息，我們可以通過以下公式來計算：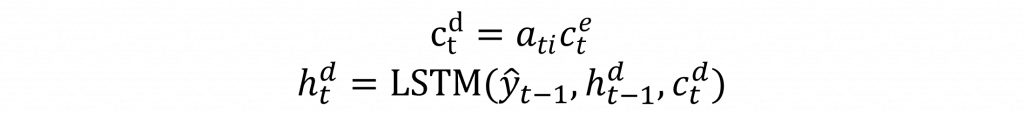

現在你是不是對於Attention機制有更深入的了解了呢？然而你可能還是有一些問題，例如c(t)是來自Encoder還是Decoder需要被計算，以及Decoder上下文向量的詳細輸入方式。為了理解這些部分，我們可以先看看圖片中的運算方式，然後再回頭查看公式，而明天我也會用程式碼的方式來加深你的印象，讓你更能夠理解這些公式的到理

總結

我相信你看到這裡，已經非常了解這些數學式的含意了。而這也是我想要傳達的概念之一：在深度學習的領域中，往往是同一公式不斷重複使用，只不過每一次技術的改良都有可能替換掉架構中的一些部份。例如，我們可能不再使用tanh來計算機率分佈，而是改用sigmoid，或者不使用加法而改用乘法來結合資訊。這些看似微小的改動，可能正是產生新模型的一個關鍵技術。因此當你理解了這些數學後，你更能做到的是根據需要改動模型，並進行優化與調整。

在這裡補充一點通常不會用乘法來結合資料，因為這樣會破壞掉正負關係，同時會導致資料之間的大小變得更大，使的模型更難運算